MA.3.3 微分中值定理

Fermat 定理和 Rolle 定理

极值

以极大值、极大值点为例
$f : U (x_{0}, δ) \to R, 若 \forall x \in U (x_{0}, δ), 都有$

f (x_{0}) \geq f (x)

$则称 f (x_{0}) 为 f 的极大值，点 x_{0} 为 f 的极大值点$

极值点与最值点的关系？

本质上无关：最值具有局部性
但是

Theorem

定义域内部的最值点一定是极值点

Fermat 定理

#Fermat定理

$设 f 在 x_{0} 取极值,$ $且 f 在 x_{0} 可导,$ $则 f^{'} (x_{0}) = 0$
Tip: $x_{0} 为 I 的一个内点 (即非端点)$

理解
- 极值点: 导数为0
几何意义
- 曲线在局部最高(低)点切线平行x轴
证明：
#驻点
- 若 $f^{'} (x_{0}) ＝ 0$ ，则称 $x_{0}$ 为函数 $f$ 的驻点
#驻点与 #极值点的关系
- Eg.1 $y = x^{3} 在 x = 0 处 : 驻点 ⇏ 极值点$ 邻域内有正负
- Eg.2 $y = | x | 在 x = 0 处 : 极值点 ⇏ 驻点$ 不可导

#Fermat引理

可导的极值点必为驻点
极值也可在不可导点取得，故
极值点必包含于驻点和不可导点中.

Rolle 定理

#Rolle定理

$设 f \in C [a, b] \cap D (a, b), 且 f (a) = f (b), 则$
$\exists ξ \in (a, b) 使得 f^{'} (ξ) = 0$

理解
- 连续可导, 怎么扭也有极值点(导数为0的时候)
几何意义
- 端点高度相同的曲线至少有一点切线平行x轴
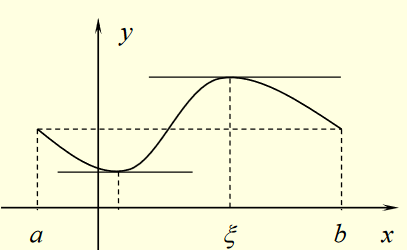
$f \in D (a, b)$ 可改为 $f \in D [a, b]$
证明
- $∵ f \in C [a, b],$ 根据 #闭区间连续函数最值性

#闭区间连续函数最值性

$若 f \in C [a, b],$ $则 f 在 [a, b] 上有最大、最小值,$ $即 \exists ξ_{1},$ $ξ_{2} \in [a, b],$ $使得$
$f (ξ_{1}) = m = min_{x \in [a, b]} f (x), f (x i_{2}) = M = max_{x \in [a, b]} f (x)$

> $令 M, m 为 f 在 [a, b] 的最大、小值$
> $若 M = m, 则 f 为常值函数, 结论显见$
> $若 M > m$
> $∵ f (a) = f (b)$
> $∴ M, m 中至少有一个 \neq f (a) = f (b)$
> $不妨设 M \neq f (a) = f (b)$
> $\Rightarrow \exists ξ \in \underset{―}{(a, b)}$
> $M = f (ξ) 在 f 内部$
> $∵ M 为最大值, f \in D [a, b]$
> 由 #Fermat引理 $f^{'} (ξ) = 0$

Example

$证明： \forall C \in R,$ $x^{3} - 3 x + C = 0 在 [0, 1] 不存在两个相异实根$

证明：（反证法）
$若 \exists x_{1} < x_{2} \in [0, 1] 均为实根$
$令 f (x) = x^{3} - 3 x + C, x \in [x_{1}, x_{2}]$
$∴ f \in D [x_{1}, x_{2}], f (x_{1}) = 0 = f (x_{2})$
根据 #Rolle定理
$\exists ξ \in (x_{1}, x_{2}) \subset [0, 1] : f^{'} (ξ) = 0$
$∵ f^{'} (ξ) = 3 ξ^{2} - 3 < 0, 矛盾$

Example

#极限的构造

$设 f \in C (a, b) \cap D (a, b),$ $且 f (a) = f (b) = 0.$
$证明 : \exists ξ \in (a, b) 使 f (ξ) + f^{'} (ξ) = 0$

Analysis:
$即证 :$
$(1 + \frac{f^{'} (x)}{f (x)}) = 0$
$\Rightarrow {(x + \ln f (x))}^{'} = 0 \dots f (x) > 0$
$\Rightarrow {(\ln e^{x} + \ln f (x))}^{'}$
$\Rightarrow {[\ln e^{x} f (x)]}_{x = ξ}^{'} \overset{d e f}{=} \ln F (x) = 0$
$\Rightarrow \ln F (x) 有驻点 \Rightarrow F (x) 有驻点$

Proof:
$F (x) := e^{x} f (x)$
$∴ F \in C [a, b] \cap D (a, b) \dots 保四则运算$
$且 F (a) = e^{a} f (a) = 0, F (b) = e^{b} f (b) = 0$
#Rolle定理
$\Rightarrow \exists ξ \in (a, b), F^{'} (ξ) = 0$
$即 : e^{x} (f (ξ) + f^{'} (ξ)) = 0$
$\Rightarrow f (ξ) + f^{'} (ξ) = 0$

#构造辅助函数

从结论出发

$e^{λ x} f (x), x^{α} f (x), \sin x f (x), \cos x f (x)$

微分中值定理

Lagrange 中值定理

#Lagrange中值定理

$设 f \in C [a, b] \cap D (a, b), 则 \exists ξ \in (a, b) 使得 :$

f^{'} (ξ) = \frac{f (b) - f (a)}{b - a}

理解
- 割线斜率等于某点斜率
- 倾斜的Rolle: 加了一个正比例函数
几何意义
- 弦AB的斜率
- 等于
- 曲线在P点切线的斜率
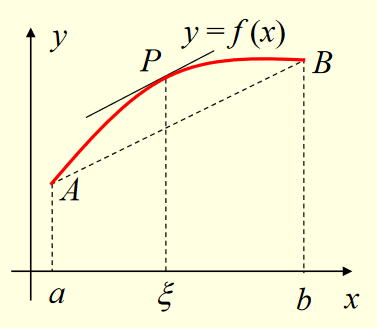
证明:

Analysis:
$即证 : {[f^{'} (x) - \frac{f (b) - f (a)}{b - a}]}_{x = ξ} = 0$
$\Rightarrow {[F (x) - ◻ x]}_{x = ξ}^{'} = 0$
$l : y = k x, A B : y = k x + b$

Proof:
$令 F (x) := f (x) - [f (a) + \frac{f (b) - f (a)}{b - a} (x - a)]$
$则 : (四则运算) F (x) \in C [a, b] \cap D (a, b) 且 F (a) = F (b) = 0$
#Rolle定理
$\exists ξ \in (a, b), F^{'} (ξ) = 0$
$即 : f^{'} (ξ) - \frac{f (b) - f (a)}{b - a} = 0$

变形: Lagrange 中值公式

#Lagrange中值公式

$f (x_{2}) - f (x_{1}) = f^{'} (ξ) (x_{2} - x_{1})$

#有限增量公式

$F (x + Δ x) - f (x) = f^{'} (x + θ Δ x) Δ x, θ \in (0, 1)$

只要 $ξ$ 介于 $x$ , $x + Δ x$ 则可
$ξ = x + θ Δ x \Leftrightarrow θ = \frac{ξ - x}{Δ x} \in (0, 1)$

常值函数

$设 I 为区间, f \in D (I), 且 f^{'} (x) = 0, 则 : f (x) = C$

Proof:

$\forall x_{1}, x_{2} \in I$
$则 : \exists ξ \in (x_{1}, x_{2}) 使 :$
#Lagrange中值公式
$f (x_{2}) - f (x_{1}) = f^{'} (x) (x_{2} - x_{1})$

导数相同

$设 I 为区间, 且 f^{'} (x) = g^{'} (x), 则 : f (x) - g (x) = C$

Lipschitz 条件

#Lipschitz条件

$若 \exists L > 0 (常数), 使 \forall x_{1}, x_{2} \in I 有$

| f (x_{2}) - f (x_{1}) | \leq L (x_{2} - x_{1})

$则称 f 在 I 上满足 L i p s c h i t z 条件$

Corollary

$设 f \in D (I), 且 f^{'} (x) 在 I 有界,$ $则 f 在 I 上满足 Lipschitz条件,$ $从而 f \in U . C (I)$

Proof:

$∵ f^{'} 有界$
$\exists L > 0, \forall x \in I, | f^{'} (x | < L$
$∴ \forall x_{1}, x_{2} \in I, \exists ξ \in (x_{1}, x_{2}) 或 (x_{2}, x_{1})$
#Lagrange中值公式
$| f (x_{2}) - f (x_{1}) | = | f^{'} (ξ) (x_{2} - f (x_{1})) | \leq L | x_{2} - x_{1} |$

Proposition

$f 在 I 上满足 L i p s c h i t z 条件 \Rightarrow f \in U . C (I)$

Proof:

$\forall ε > 0, \exists δ > 0, (不妨取 δ = \frac{L}{ε})$
$使 \forall x_{1}, x_{2} \in I, 且 | x_{2} - x_{1} | < δ :$
$| f (x_{2}) - f (x_{1}) | \leq L | x_{2} - x_{1} | \leq ε$

Question

$L i p s c h i t z \overset{?}{\leftarrow} U . C$
$L i p s c h i t z \overset{?}{\to} 导数有界$

Example

$判断 f (x) = \sqrt{x} 在 [1, \infty) 上的一致连续性$

证明 $f^{'}$ 有界即可

$证明恒等式 \arcsin x + \arccos x = \frac{π}{2}$

$f^{'} = 0 \to x := 0$

Corollary

$f^{'} (x) = 0 在开区间成立, 但在闭区间连续$ $\Rightarrow f^{'} (x) = 0 可以推广到闭区间$

Cauchy 定理

#Cauchy中值定理

$设 f, g \in C [a, b] \cap D (a, b),$ $且 \forall x \in (a, b), g^{'} (x) \neq 0,$ $则 \exists ξ \in (a, b) 使$

\frac{f (b) - f (a)}{g (b) - g (a)} = \frac{f^{'} (ξ)}{g^{'} (ξ)}

理解
- $若 g (x) = x 则为 L a g r a n g e 定理$
- 重点在于取同一个 $ξ$ (at the same time)
证明

$即证 : {[f^{'} (x) - \frac{f (b) - f (a)}{g (b) - g (a)} g^{'} (x)]}_{x = ξ} = 0$
$即证 : {[f (x) - \frac{f (b) - f (a)}{g (b) - g (a)} g (x)]}_{x = ξ}^{'} = 0$
$令 F (x) :=$ ${[(f (x) - f (a)) - \frac{f (b) - f (a)}{g (b) - g (a)} (g (x) - g (a))]}_{x = ξ} = 0$
#Rolle定理
$\exists ξ \in (a, b) : F^{'} (ξ) = 0$
$即 : f^{'} (ξ) - \frac{f (b) - f (a)}{g (b) - g (a)} g^{'} (x) = 0$

Example

$0 < a < b, f \in C [a, b] \cap D (a, b) . 证明 : \exists ξ \in (a, b),$ $使 :$

f (b) - f (a) = ξ f^{'} (ξ) \ln \frac{b}{a}

$\Rightarrow \frac{f (b) - f (a)}{\ln b - \ln a} = \frac{f^{'} (ξ)}{\frac{1}{ξ}}$

导函数的性质

Intro

$f (x) = {\begin{cases} \ln (1 + 2 x) & x > 0 \\ \sin x & x \leq 0 \end{cases}, f_{+}^{'} (0) = ? .$

Solution.1:
$定义 : lim_{x \to 0^{+}} \frac{f (x) - f (0)}{x - 0} = lim_{x \to 0^{+}} \frac{\ln (1 + 2 x) - 0}{x} = 2$
Solution.2:(WRONG!)
$x > 0 : f^{'} (x) = \frac{2}{1 + 2 x} \Rightarrow f_{+}^{'} (0) = lim_{x \to 0^{+}} \frac{2}{1 + 2 x} = 2$

很遗憾, 若 $f (0) \neq 0$ , 此时Solution1极限不存在, 但Solution2仍然能算出(错)解

导函数极限与导数的关系

#导数极限定理

$设 f 在 x_{0} 右连续,$ $在 (x_{0}, x_{0} + δ) 可导,$ $若 lim_{x \to x_{0}^{+}} f^{'} (x) = l,$ $则 f 在 x_{0} 右可导,$ $且 f_{+}^{'} (x_{0}) = l$

左导数类似

理解
证明
Proof

$∵ f \in C [x_{0}, x] \cap D (x_{0}, x)$
$∴ \exists ξ_{x} \in (x_{0}, x) \dots ξ 依赖于 x$
#Lagrange中值公式
$∵ \frac{f (x) - f (x_{0})}{x - x_{0}} = f^{'} (ξ_{x})$
$\begin{aligned} ∴ lim_{x \to x_{0}^{+}} \frac{f (x) - f (x_{0})}{x - x_{0}} & = lim_{x \to x_{0}^{+}} f^{'} (ξ_{x}) \\ = lim_{ξ \to x_{0}^{+}} f^{'} (ξ_{x}) \\ = l \end{aligned}$

且慢

graph LR
右连续 -- 满足 --> 右可导 -- 满足 --> 右导数=导函数极限
右连续 -- 不满足 --> 不可导
右可导 -- 不满足 --> 不可导

Review: 连续、可导、导函数

单侧连续：函数单侧极限存在；单侧极限等于函数值
连续：函数（左右）极限存在，（左右）极限等于函数值
不连续：极限不存在 or 极限存在但不等于函数值
右可导：右侧△y/△x极限存在
可导：（左右）△y/△x的极限存在且相等
- 加粗的条件说明：左可导，右可导，未必可导
- 特别地
  - 对于某一点，导数存在就是指可导
  - 对于某邻域，导数存在和可导不是一个概念:邻域可导要求邻域内每一点导数都存在
- 开区间连续，闭区间可导
  - 闭区间可导就是
    在这个区间上导数处处存在
导函数：导函数本质上是个函数，导数则是极限的定义得出，因此不能在某些场合（尤其是在分段、间断处）使用导函数的极限为导数
- ~~右连续（其实是冗余的）+~~右可导=右导数为导函数极限
- ~~左右连续（其实是冗余的）+~~可导（导数相等)=导数为导函数极限
  - =>可导处的导函数等于导数
导函数连续：在可导的基础上，该导函数两侧极限存在且等于该处导函数的值

无第一类间断点

Corollary

$设 f \in D (a, b),$ $则 f^{'} (x) 在 (a, b) 内无第一类间断点$

开区间连续函数的导数无第一类间断点

Proof:

(反证法)
$若 \exists x_{0} \in (a, b) 是第一类间断点$
$∴ lim_{x \to x_{0}^{-}} f^{'} (x) = l_{1}, lim_{x \to x_{0}^{+}} f^{'} (x) = l_{2}$
$∵ f 在 x_{0} 可导 \Rightarrow f 连续$
$∴ f_{-}^{'} (x_{0}) = l_{1}, f_{+}^{'} (x_{0}) = l_{2}$
$∵ f 在 x_{0} 可导$
$∴ f_{+}^{'} (x_{0}) = f_{-}^{'} (x_{0}) = f^{'} (x_{0})$
$i.e. l_{1} = l_{2} = f^{'} (x_{0})$
$∴ lim_{x \to x_{0}} f^{'} (x) = f^{'} (x_{0}) \Rightarrow 连续, 矛盾$

"零值性" / Darboux 定理

#Darboux定理

$设 f \in D [a, b],$ $且 f^{'} (a) \cdot f^{'} (b) < 0,$ $则 : \exists ξ \in (a, b), 使$

f^{'} (ξ) = 0

Proof:

$不妨 f_{+}^{'} (a) > 0, f_{-}^{'} (b) < 0$
$∴ f_{+}^{'} (a) = lim_{x \to a^{+}} \frac{f (x) - f (a)}{x - a} > 0$
#极限局部保号性
$\exists δ_{1} > 0,$ $\forall x \in (a, a + δ_{1}) 有 :$
$\frac{f (x) - f (a)}{x - a} > 0 \dots 取绝对值$
$取 x = x_{1} \in (a, a + δ), 则 : \frac{f (x_{1}) - f (a)}{x_{1} - a} > 0$
$\Rightarrow f (x_{1}) > f (a)$
$同理 : f (x_{2}) > f (b)$
$又 ∵ f \in C [a, b],$ $∴ \exists ξ \in [a, b] 使 f (ξ) = max_{a \leq x \leq b} {f (x)}$
$注意 : f (ξ) \geq {\begin{cases} f (x_{1} > f (a) \\ f (x_{2}) > f (b) \end{cases}$
$\Rightarrow ξ (a, b) 从而 f (ξ) 极大值$
#Fermat定理
$f^{'} (ξ) = 0$

"介值性"

#导函数介值性

$设 f \in D [a, b],$ $且 f^{'} (a) < f^{'} (b),$ $则 : \forall λ \in (f^{'} (a), f^{'} (b)),$ $\exists ξ \in (a, b), 使$

f^{'} (ξ) = λ

理解
- 导函数未必连续, 但有介值性
- $f^{'} (x)$ 可取介于端点导数值的所有值至少一次
证明

Proof:
$令 F (x) := f (x) - λ x$
$x \in [a, b], 则 F \in D [a, b], 且$
$F^{'} (a) = f^{'} (a) - λ < 0, F^{'} (b) = f^{'} (b) - λ > 0$
#Darboux定理
$\exists ξ \in (a, b)$
$F^{'} (ξ) = 0$
$即 : f (ξ) = λ$

Fermat 定理 和 Rolle 定理

极值

Fermat 定理

证明：

Rolle 定理

Analysis: 即证即证: (1+f′(x)f(x))=0 ⇒(x+ln⁡f(x))′=0⋯f(x)>0 ⇒(ln⁡ex+ln⁡f(x))′ ⇒[ln⁡exf(x)]x=ξ′=defln⁡F(x)=0 有驻点有驻点⇒ln⁡F(x)有驻点⇒F(x)有驻点

微分中值定理

Lagrange 中值定理

变形: Lagrange 中值公式

Lipschitz 条件

Cauchy 定理

导函数的性质

导函数极限与导数的关系

Review: 连续、可导、导函数

无第一类间断点

"零值性" / Darboux 定理

"介值性"

Fermat 定理和 Rolle 定理

Analysis:
$即证 :$
$(1 + \frac{f^{'} (x)}{f (x)}) = 0$
$\Rightarrow {(x + \ln f (x))}^{'} = 0 \dots f (x) > 0$
$\Rightarrow {(\ln e^{x} + \ln f (x))}^{'}$
$\Rightarrow {[\ln e^{x} f (x)]}_{x = ξ}^{'} \overset{d e f}{=} \ln F (x) = 0$
$\Rightarrow \ln F (x) 有驻点 \Rightarrow F (x) 有驻点$